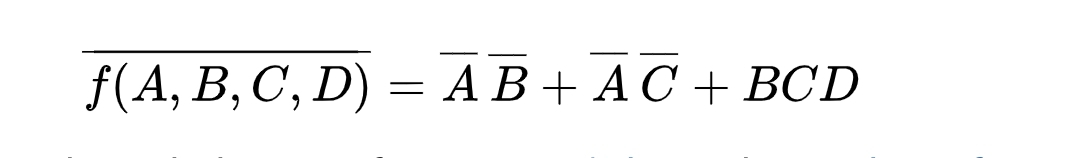𝐤𝐚𝐫𝐧𝐚𝐠𝐡 𝐌𝐚𝐩

      𝐊𝐚𝐫𝐧𝐚𝐮𝐠𝐡 𝐦𝐚𝐩

                       The Karnaugh map (KM or K-map) is a method of simplifying Boolean algebra expressions. Maurice Karnaugh introduced it in 1953[1][2] as a refinement of Edward W. Veitch's 1952 Veitch chart,[3][4] which actually was a rediscovery of Allan Marquand's 1881 logical diagram[5] aka Marquand diagram'[4] but with a focus now set on its utility for switching circuits.'[4] Veitch charts are therefore also known as Marquand–Veitch diagrams,'[4] and Karnaugh maps as Karnaugh–Veitch maps (KV maps).

          An example Karnaugh map. This image actually shows two Karnaugh maps: for the function ƒ, using minterms (colored rectangles) and for its complement, using maxterms (gray rectangles). In the image, E() signifies a sum of minterms, denoted in the article as {\displaystyle \sum m_{i}}{\displaystyle \sum m_{i}}.

The Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability.[1] It also permits the rapid identification and elimination of potential race conditions.

The required Boolean results are transferred from a truth table onto a two-dimensional grid where, in Karnaugh maps, the cells are ordered in Gray code,[6][4] and each cell position represents one combination of input conditions, while each cell value represents the corresponding output value. Optimal groups of 1s or 0s are identified, which represent the terms of a canonical form of the logic in the original truth table.[7] These terms can be used to write a minimal Boolean expression representing the required logic.

Karnaugh maps are used to simplify real-world logic requirements so that they can be implemented using a minimum number of physical logic gates. A sum-of-products expression can always be implemented using AND gates feeding into an OR gate, and a product-of-sums expression leads to OR gates feeding an AND gate.[8] Karnaugh maps can also be used to simplify logic expressions in software design. Boolean conditions, as used for example in conditional statements, can get very complicated, which makes the code difficult to read and to maintain. Once minimised, canonical sum-of-products and product-of-sums expressions can be implemented directly using AND and OR logic operators.[9] Diagrammatic and mechanical methods for minimizing simple logic expressions have existed since at least the medieval times. More systematic methods for minimizing complex expressions began to be developed in the early 1950s, but until the mid to late 1980s the Karnaugh map was the most common used in practice.

Karnaugh maps are used to facilitate the simplification of Boolean algebra functions. For example, consider the Boolean function described by the following truth table.

Truth table of a function

	A	B	C	D	$𝑓(A,B,C,D)}$
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

Following are two different notations describing the same function in unsimplified Boolean algebra, using the Boolean variables A, B, C, D, and their inverses.

• ${\displaystyle f(A,B,C,D)=\sum _{}m_{i},i\in \{6,8,9,10,11,12,13,14\}}$ where ${\displaystyle m_{i}}$ are the minterms to map (i.e., rows that have output 1 in the truth table).
• ${\displaystyle f(A,B,C,D)=\prod _{}M_{i},i\in \{0,1,2,3,4,5,7,15\}}$ where ${\displaystyle M_{i}}$ are the maxterms to map (i.e., rows that have output 0 in the truth table).

Karnaugh map

K-map drawn on a torus, and in a plane. The dot-marked cells are adjacent.

K-map construction. Instead of the output values (the rightmost values in the truth table), this diagram shows a decimal representation of the input ABCD (the leftmost values in the truth table), therefore it is not a Karnaugh map.

In three dimensions, one can bend a rectangle into a torus.

In the example above, the four input variables can be combined in 16 different ways, so the truth table has 16 rows, and the Karnaugh map has 16 positions. The Karnaugh map is therefore arranged in a 4 × 4 grid.

The row and column indices (shown across the top, and down the left side of the Karnaugh map) are ordered in Gray code rather than binary numerical order. Gray code ensures that only one variable changes between each pair of adjacent cells. Each cell of the completed Karnaugh map contains a binary digit representing the function's output for that combination of inputs.

After the Karnaugh map has been constructed, it is used to find one of the simplest possible forms — a canonical form — for the information in the truth table. Adjacent 1s in the Karnaugh map represent opportunities to simplify the expression. The minterms ('minimal terms') for the final expression are found by encircling groups of 1s in the map. Minterm groups must be rectangular and must have an area that is a power of two (i.e., 1, 2, 4, 8...). Minterm rectangles should be as large as possible without containing any 0s. Groups may overlap in order to make each one larger. The optimal groupings in the example below are marked by the green, red and blue lines, and the red and green groups overlap. The red group is a 2 × 2 square, the green group is a 4 × 1 rectangle, and the overlap area is indicated in brown.

The cells are often denoted by a shorthand which describes the logical value of the inputs that the cell covers. For example, AD would mean a cell which covers the 2x2 area where A and D are true, i.e. the cells numbered 13, 9, 15, 11 in the diagram above. On the other hand, AD would mean the cells where A is true and D is false (that is, D is true).

The grid is toroidally connected, which means that rectangular groups can wrap across the edges (see picture). Cells on the extreme right are actually 'adjacent' to those on the far left, in the sense that the corresponding input values only differ by one bit; similarly, so are those at the very top and those at the bottom. Therefore, AD can be a valid term—it includes cells 12 and 8 at the top, and wraps to the bottom to include cells 10 and 14—as is BD, which includes the four corners.

Solution

Diagram showing two K-maps. The K-map for the function f(A, B, C, D) is shown as colored rectangles which correspond to minterms. The brown region is an overlap of the red 2×2 square and the green 4×1 rectangle. The K-map for the inverse of f is shown as gray rectangles, which correspond to maxterms.

Once the Karnaugh map has been constructed and the adjacent 1s linked by rectangular and square boxes, the algebraic minterms can be found by examining which variables stay the same within each box.

For the red grouping:

• A is the same and is equal to 1 throughout the box, therefore it should be included in the algebraic representation of the red minterm.
• B does not maintain the same state (it shifts from 1 to 0), and should therefore be excluded.
• C does not change. It is always 0, so its complement, NOT-C, should be included. Thus, C should be included.
• D changes, so it is excluded.

Thus the first minterm in the Boolean sum-of-products expression is AC.

For the green grouping, A and B maintain the same state, while C and D change. B is 0 and has to be negated before it can be included. The second term is therefore AB. Note that it is acceptable that the green grouping overlaps with the red one.

In the same way, the blue grouping gives the term BCD.

The solutions of each grouping are combined: the normal form of the circuit is 

.

Thus the Karnaugh map has guided a simplification of

It would also have been possible to derive this simplification by carefully applying the axioms of boolean algebra, but the time it takes to do that grows exponentially with the number of terms.

Inverse

The inverse of a function is solved in the same way by grouping the 0s instead.

The three terms to cover the inverse are all shown with grey boxes with different colored borders:

This yields the inverse:

Through the use of De Morgan's laws, the product of sums can be determined:

Don't cares

The value of $f(A,B,C,D)$ for ABCD = 1111 is replaced by a "don't care". This removes the green term completely and allows the red term to be larger. It also allows blue inverse term to shift and become larger

Karnaugh maps also allow easier minimizations of functions whose truth tables include "don't care" conditions. A "don't care" condition is a combination of inputs for which the designer doesn't care what the output is. Therefore, "don't care" conditions can either be included in or excluded from any rectangular group, whichever makes it larger. They are usually indicated on the map with a dash or X.

The example on the right is the same as the example above but with the value of f(1,1,1,1) replaced by a "don't care". This allows the red term to expand all the way down and, thus, removes the green term completely.

This yields the new minimum equation:

Note that the first term is just A, not AC. In this case, the don't care has dropped a term (the green rectangle); simplified another (the red one); and removed the race hazard (removing the yellow term as shown in the following section on race hazards).

The inverse case is simplified as following.