Number system
NUMBER SYSTEM
When we type some letters or words, the computer translates them in numbers as computers can understand only numbers. A computer can understand the positional number system where there are only a few symbols called digits and these symbols represent different values depending on the position they occupy in the number.
The value of each digit in a number can be determined using −
The digit
The position of the digit in the number
The base of the number system (where the base is defined as the total number of digits available in the number system)
DIFFERENT TYPE OF NUMBER SYSTEM
The classification of numbers systems on the basis of base can be understood from the below diagram.
| Number system | Base | Used digits |
|---|---|---|
| Binary | 2 | 0,1 |
| Octal | 8 | 0,1,2,3,4,5,6,7 |
| Decimal | 10 | 0,1,2,3,4,5,6,7,8,9 |
| Hexadecimal | 16 | 0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F |
A link that describes the above,
https://youtu.be/32Kwy3GWQWc
or
BINARY NUMBER SYSTEM
. The modern computers do not process the decimal numbers.
. They only work with a binary number system.
. It uses only two digits 0 and 2.
. The base of binary number system is 2 because it has only two digits.
. The digital electronics equipment's are works on the binary number system.
EXAMPLE;
DECIMAL NUMBER SYSTEM
.The number system is having digit 0,1,2,3,4,5,6,7,8,9.
. Total ten digits are involved. So that base of the decimal number system is 10.
EXAMPLE;
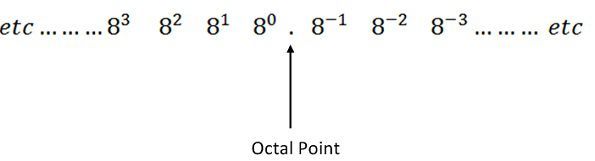
OCTAL NUMBER SYSTEM
.Uses eight digits 0,1,2,3,4,5,6,7.
. Also called '' base 8 number system''
. Each position in an octal number represents a 0 power of the base (8)
EXAMPLE;
HEXADECIMAL NUMBER SYSTEM
.These4 numbers are used extensively in microprocessor.
.The hexadecimal number system has a base of 16.
.It consists of the following sixteen numbers of digits ( 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F )
.Letters represents number starting from
A=10
B=11
C=12
D=13
E=14
F=15
G=16
EXAMPLE;